Time And Space – The Last Algorithms Course You'll Need

The very first thing we tackle

Time and Space. Big O as they call it.

What is Big O

Big O is a way to categorize your algorithms time or memory requirements based on input. It is not meant to be an exact measurement. It will not tell you how many CPU cycles it takes, instead it is meant to generalize the growth of your algorithm.

Example

So when someone says Oh of N, they mean your algorithm will grow linearily based on input.

Why do we use it?

Often it will help us make decisions about what data structures and algorithms to use. Knowing how they will perform can greatly help create the best possible program out there.

So lets do a small example

First, Lets consider the following code.

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }

    return sum;
}

For those that know big o, this is easy

But those who have never even classified a function, this may be a complete mystery. That is fine.

Big O, said differently

As your input grows, how fast does computation or memory grow?

Important concepts

growth is with respect to the input

In the real world

obviously memory growing is not computationally free, but in the matter of thinking about algorithms, we don't necessarily think about that.

In languages like Go or JavaScript you pay even heavier penalties because the memory can be kept around, grows faster, and causes complete halts in your program for cleanup.

Lets go back to our example

Lets look at input. How does our program's execution time grow with respect to input?

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }

    return sum;
}

Me> It may or may not be obvious, but we have an N relationship. O(N) time complexity

You> How can you tell?

Simplest trick for complexity

Look for loops

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }

    return sum;
}

What's the running time

If the previous was O(N), what's this?

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }

    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }

    return sum;
}

It 2N?

Important concepts

growth is with respect to the input
Constants are dropped

O(2N) -> O(N) and this makes sense. That is because Big O is meant to describe the upper bound of the algorithm (the growth of the algorithm). The constant eventually becomes irrelevant.

Take the following:

N = 1, O(10N) = 10, O(N^2) = 1

N = 5, O(10N) = 50, O(N^2) = 25

N = 100, O(10N) = 1,000, O(N^2) = 10,000 // 10x bigger

N = 1000, O(10N) = 10,000, O(N^2) = 1,000,000 // 100x bigger

N = 10000, O(10N) = 100,000, O(N^2) = 100,000,000 // 1000x bigger

There is practical vs theoretical differences

Just because N is faster than N^2, doesn't mean practically its always faster for smaller input.

Remember, we drop constants. Therefore O(100N) is faster than O(N^2) but practically speaking, you would probably win for some small set of input.

Lets do another example

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        const charCode = n.charCodeAt(i);
        // Capital E
        if (charCode === 69) {
            return sum;
        }

        sum += charCode;
    }

    return sum;
}

In BigO we often consider the worst case

Especially in interviews (i have never been asked for best, average, and worst case, just worst case).

E = 69

Therefore any string with E in it will terminate early (unless E is the last item in the list).

ITS STILL O(N)

Important concepts

growth is with respect to the input
Constants are dropped
Worst case is usually the way we measure,

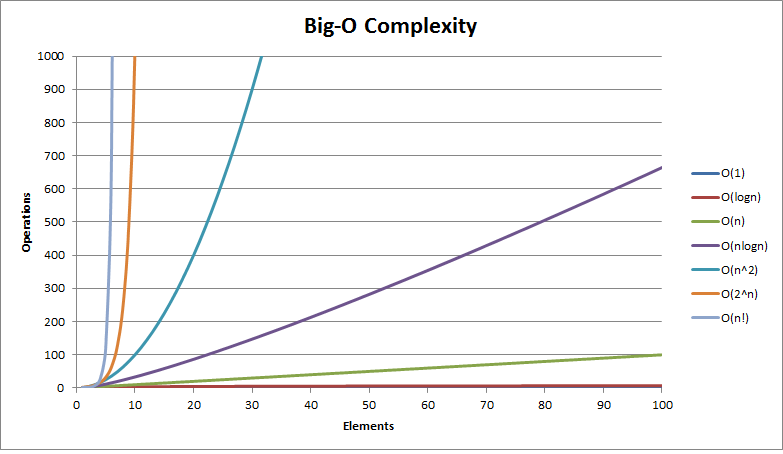
The common complexities

Source Big O Notation

Some examples

O(N^2)

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        for (let j = 0; j < n.length; ++j) {
            sum += charCode;
        }
    }

    return sum;
}

O(N^3)

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        for (let j = 0; j < n.length; ++j) {
            for (let k = 0; k < n.length; ++k) {
                sum += charCode;
            }
        }
    }
    return sum;
}

O(n log n)

Quicksort (we will implement and explain)

O(log n)

Binary search trees

There is one time that we will see today, that hasn't been mentioned

O(sqrt(n))

Why so obviated?

There are other resources out there to dive deep into big o notation. And I just don't think we need Yet Another Big O explanation. Instead I am going to focus on actively looking at running times and we will determine things together.

Important concepts

growth is with respect to the input
Constants are dropped
Worst case is usually the way we measure

One more note

Is there anything else besides Big O? Well, there is technically a bunch of different ways to measure the complexity of algorithms, but in general the easiest one to use is the "Upper Bound"

Space the Final Frontier

We pretty much wont be going over space in this course. Just not something we will be discussing. I find this less consequetial in daily life considering I see things like this.

// or whatever it is in react
// O(N) time + O(N) space!  COUNT ME IN
return <Component
            ...props />

Before we go

Questions?

← Previous Next →